Controlling a CRC-32 hash

mathematics / hacking

Mon, Dec 20, 21

Today, we are going to see why CRC32 is utterly broken as a crypto hash (which it is **not**!), and demonstrate a clever way to control CRC32 string hashes by only altering the case. This is for fun and giggles, I'm pretty sure nobody today uses CRC to protect files against *intentional* data alteration, but it's a good occasion to do some linear algebra in the Galois field of order 2.

I am not the original author of this method, I just read about it a few years ago in a random comment thread buried somewhere and decided to have a go at implementing the idea. My original implementation was in Matlab, but I thought a C++ implementation would be a bit clearer as far as bit operations are concerned. As we perform some -apprentice level- binary wizardry, it is not the most readable thing in the end, but I guess you had it coming for clicking on such an article title!

Disclaimer: I am by no means a mathematician and the maths being shown here are far from rigorous. Even though the implementation ends up working great, take the formulas cum grano salis. And by any means, don’t hesitate to contact me if you think you can help improve this article in that regard. That being said, let’s dive in!

Cyclic Redundancy Check

A Cyclic Redundancy Check or CRC, is an error detection code, used in low level transport protocols and storage devices to detect accidental data corruption due to the noise inherent to the communication channel. A CRC is basically a checksum that is forwarded or stored alongside a data block, so the block can be checked for integrity after retrieval. It is based on cyclic codes, hence its name, so it is a polynomial code. As such, a CRC is generated as the remainder of a polynomial long division, the data block interpreted as a series of polynomial coefficients being the dividend, and the divisor being a fixed so-called generator polynomial. This division can be efficiently implemented in $O (n)$ time, making this detection code really fast. Polynomial operations are carried over a finite field, and in general the Galois field $F_{2}$ of two elements (named $0$ and $1$ for convenience) is used.

To labor the point, any binary string (of zeros and ones) can be viewed as a polynomial over $F_{2}$ : for instance, the string $1011$ can be mapped to the polynomial $P (x) = 1 x^{0} + 1 x^{1} + 0 x^{2} + 1 x^{3} = 1 + x + x^{3}$ . Note how the coefficients match the data, and the powers match the index in the binary string. The bit ordering is a matter of personal preference, here we chose to map the least significant bit to the coefficient of the lowest power of $x$ .

The most popular CRC is CRC32, which is 32-bit long. So theory shows that it can be employed to detect burst errors of size 32 at most. Here is an implementation that we’ll use:

uint32_t crc32(const char *data, size_t len)
{
    uint32_t crc = init_xor;
    for (size_t ii = 0; ii < len; ++ii)
    {
        crc ^= uint32_t(data[ii]);
        for (size_t jj = 0; jj < 8; ++jj)
        {
            uint32_t mask = (crc & 1) ? ~(crc & 1) + 1 : 0;
            crc = (crc >> 1) ^ (polynomial & mask);
        }
    }
    crc = ~crc;
    return crc;
}

CRC satisfies an affine property. Let’s denote by $\oplus$ the bitwise XOR operation (vector addition over $F_{2}$ ). Given two binary strings $x$ and $y$ , we have:

\begin{matrix} (1) & C R C (x \oplus y) = C R C (x) \oplus C R C (y) \oplus C \end{matrix}

Where $C$ is a constant that depends only on the lengths of $x$ and $y$ .

The problem

Say we have an input character string $S$ of size at least 32 (it will be important later on). We only consider mixed-case strings consisting only of alphabetical characters, for the sake of simplicity. Its CRC32 is a 32-bit word denoted by $C R C (S)$ . We would like to find a series of substitutions to apply to $S$ , producing an altered string $S^{'}$ such that $C R C (S^{'})$ evaluates to a target value we know beforehand. If we succeed in doing so, we will have shown that the CRC-32 checksum can be controlled.

Elementary transformations

Let’s restrain ourselves to case substitutions, so the output string $S^{'}$ stays readable. We will denote by $U^{i}$ the elementary transformation which toggles the case of the $i$ -th character in the string. For example, if $S = “HelloWorld”$ , then $U^{1} S = “HElloWorld”$ and $U^{5} S = “Helloworld”$ . Note that in ASCII, such a transformation translates to adding / subtracting 32 to the target character value (e.g. $‘A’ = 65 \mapsto ‘a’ = 97$ ), meaning that only the bit of index 5 of the character value will be toggled. Such an elementary transformation will however flip multiple bits in the CRC. But maybe by applying multiple transformations $U^{i}$ we can flip a single bit?

By convention, we regard the algebra of the transformations $U^{i}$ as written additively. There is no harm in doing so, because all the $U^{i}$ commute (e.g. toggling the case of the first character then the third gives the same result as toggling the case of the third then the first). Then, for instance, $(U^{0} + U^{2}) S = (U^{2} + U^{0}) S = “heLloWorld”$ . Additionally, a transformation $U^{i}$ can be multiplied by a scalar of $F_{2}$ : a coefficient $α_{i} \in F_{2}$ equal to one means that $U^{i}$ is applied, and conversely, a coefficient of zero means that the corresponding elementary transformation is not applied. Moreover, the $U^{i}$ are linearly independent (as there is no way to toggle the case of the $i$ -th character by toggling the case of other characters elsewhere), and they span the whole space $U$ of possible string substitutions (as any composite case substitution can be written as a sum of elementary transformations). So they form a basis $B$ of $U$ which is a vector space over $F_{2}$ . Complicated phrasing, simple stuff.

Suppose now, that composite transformations that toggle a single bit in the CRC exist (and we have reasons to think that they do, as CRC is affine). As elements of $U$ , they can be written as linear combinations of elementary case transformations:

\begin{matrix} (2) & V^{j} = \sum_{i = 0}^{31} α_{i}^{j} U^{i}, α_{i}^{j} \in F_{2} \end{matrix}

Here, the upstairs index $j$ indicates that this transformation will flip only the $j$ -th bit in the CRC. There are 32 such transformations as there are only 32 bits to be flipped in a CRC-32 checksum, so $j \in ⟦ 0, 31 ⟧$ . The transformations $V^{j}$ can be viewed as another kind of elementary transformations! They too are linearly independent as flipping a single bit in the CRC cannot be reproduced by flipping other bits elsewhere. But answering the question as to whether they span $U$ and form an actual basis is tricky.

Diffs

As we’ve seen, given an input string $S$ , $C R C (U^{i} S)$ has multiple bits flipped when compared to $C R C (S)$ . Then, the binary string $D^{i} = C R C (S) \oplus C R C (U^{i} S)$ which we call a diff will have ones at the positions where the bits are flipped. Using the diffs, we can convince ourselves that $1$ is true. Denote by $M^{i}$ the binary string of same length than $S$ , consisting in zeros everywhere except at position 5 of the $i$ -th byte where there is a one. Then we have:

\begin{matrix} (3) & U^{i} S = S \oplus M^{i} \end{matrix}

Injecting this into $1$ , we get:

\begin{matrix} (4) & C R C (U^{i} S) = C R C (S \oplus M^{i}) = C R C (S) \oplus C R C (M^{i}) \oplus C \end{matrix}

Then, by definition of $D^{i}$ :

\begin{matrix} (5) & \begin{aligned} D^{i} & = C R C (S) \oplus C R C (U^{i} S) \\ = C R C (S) \oplus C R C (S) \oplus C R C (M^{i}) \oplus C \\ = C R C (M^{i}) \oplus C \end{aligned} \end{matrix}

Then, we could compute the sum $D^{i} \oplus C R C (M^{i})$ for multiple values of $i$ , and we would find that it always returns the same value $C$ :

inline char toggle_case(char input)
{
    if (std::isalpha(input))
        return std::islower(input) ? char(std::toupper(input)) : char(std::tolower(input));
    return input;
}

std::vector<char> gen_mask(size_t idx, size_t len)
{
    std::vector<char> ret(len, 0);
    ret[idx] = 1 << 5;
    return ret;
}

int main(int argc, char **argv)
{
    std::string input = "HelloWorld";

    for (size_t ii = 0; ii < input.size(); ++ii)
    {
        std::string alt(input);
        alt[ii] = toggle_case(alt[ii]);
        auto M = gen_mask(ii, input.size());

        uint32_t diff = crc32(input.data(), input.size()) ^ crc32(alt.data(), alt.size());
        uint32_t C = diff ^ crc32(M.data(), M.size());
        std::cout << std::bitset<32>(C) << std::endl;
    }

    return 0;
}

This simple program outputs the same value 11100011100010100110100001110110 multiple times. This is our constant $C$ for the string $S = “HelloWorld”$ .

Now, let’s consider $C R C (V^{j} S)$ . By virtue of $1$ , $2$ and $3$ , we have:

\begin{matrix} (6) & \begin{aligned} C R C (V^{j} S) & = C R C ((\sum_{i} α_{i}^{j} U^{i}) S) \\ = C R C (S \oplus α_{0}^{j} M^{0} \oplus α_{1}^{j} M^{1} \oplus \dots \oplus α_{N - 1}^{j} M^{N - 1}) \\ = C R C (S) \oplus ⨁_{i} α_{i}^{j} (C R C (M^{i}) \oplus C) \end{aligned} \end{matrix}

The $α_{i}^{j}$ pass through the CRC, because a transformation that is not applied ( $α_{i}^{j} = 0$ ) issues a zero term in the big XOR sum, so they might as well be factored out. Also, each time we extract a term from the CRC, the same constant $C$ comes with it (as $S$ and all the $M^{i}$ have the same length). Substituting $5$ we get:

\begin{matrix} (7) & C R C (V^{j} S) = C R C (S) \oplus ⨁_{i} α_{i}^{j} D^{i} \end{matrix}

And so, if we write $D_{V}^{j} = C R C (S) \oplus C R C (V^{j} S)$ we finally obtain:

\begin{matrix} (8) & D_{V}^{j} = ⨁_{i} α_{i}^{j} D^{i} \end{matrix}

This shows that the diffs corresponding to the transformations $V^{j}$ are in fact linear combinations of the diffs corresponding to the elementary transformations $U^{i}$ . It seems an awful lot like we need to pack the $D^{i}$ s in a matrix, and Gauss-Jordan the heck out of it. As there are 32 $D_{V}^{j}$ s to compute, we need at least 32 $D^{i}$ s to have a chance at solving this linear algebra problem, that’s why we require a string of length at least 32.

Solution

Computing the diffs

First, let’s define a structure to contain our diff matrix. Instead of using an array of zeros and ones, we pack all the data into an unsigned integer of size 32. It will simplify a lot matrix operations, albeit being harder to read. As we are going to perform a Gauss-Jordan elimination on the diff matrix, we also need to store a transfer matrix. I chose to pack them together (like we do on paper with an augmented matrix), it makes it easier to broadcast column operations to both of them this way:

struct Column
{
    uint32_t diff;
    uint64_t transfer;
};

To compute the diffs, we run along the string toggling the case of each character one by one:

void compute_diffs(const std::string &init_str, std::vector<Column> &columns)
{
    columns.resize(init_str.size());
    uint32_t init_crc = crc32(init_str);

    for (size_t ii = 0; ii < init_str.size(); ++ii)
    {
        // Singular case modification at index ii
        std::string tmp(init_str);
        tmp[ii] = toggle_case(tmp[ii]);

        // Record diff for this transformation
        columns[ii].diff = init_crc ^ crc32(tmp);
        // The transfer matrix is the identity in this basis
        columns[ii].transfer = 1ul << ii;
    }
}

The transfer matrix is also initialized to identity during this pass. Yes, the 1 << ii is going to overflow past 63, yielding all-zeros columns, but it’s not going to matter in the end.

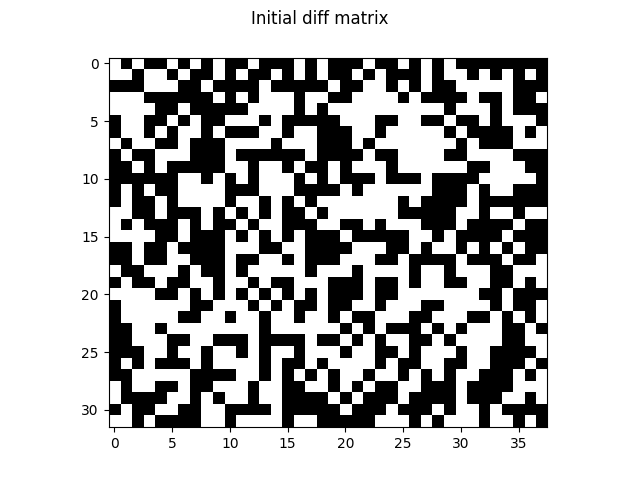
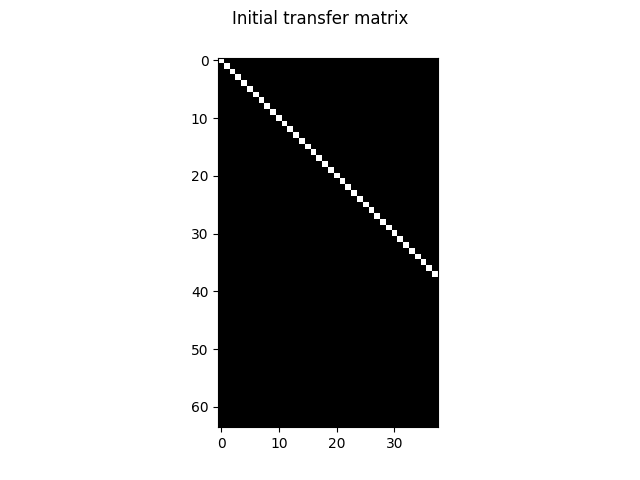
Here is how the diff and transfer matrices look like after calling the above function.

Gauss-Jordan elimination in $F_{2}$

Because the addition in $F_{2}$ is $m o d 2$ , writing a Gaussian elimination is not that much of an ordeal:

void diagonalize(std::vector<Column> &columns)
{
    // Use a GF(2)-Gauss-Jordan elimination to diagonalize the diffs and
    // apply the same operations to the transfer matrix

    for (size_t cur_column = 0; cur_column < columns.size(); ++cur_column)
    {
        // Get the index of the first set bit in this column (pivot)
        uint32_t col_mask = columns[cur_column].diff & ~(columns[cur_column].diff - 1);
        // For all other columns, find 1s in the column where the pivot is found
        for (size_t other_column = 0; other_column < columns.size(); ++other_column)
        {
            if (other_column != cur_column && (columns[other_column].diff & col_mask) > 0)
            {
                // If found, add the pivot column to this column to clear the 1
                columns[other_column].diff ^= columns[cur_column].diff;
                // Same operation on transfer matrix
                columns[other_column].transfer ^= columns[cur_column].transfer;
            }
        }
    }
}

Note that we perform elementary column operations rather than elementary row operations. Also note how the same operations are applied to the transfer matrix. I used this paper as a source for the implementation:

A Fast Algorithm for Gaussian Elimination over GF(2) and its Implementation on the GAPP, Çetin K. Koç and Sarath N. Arachchige, Journal of Parallel and Distributed Computing 13, 118-122 (1991)

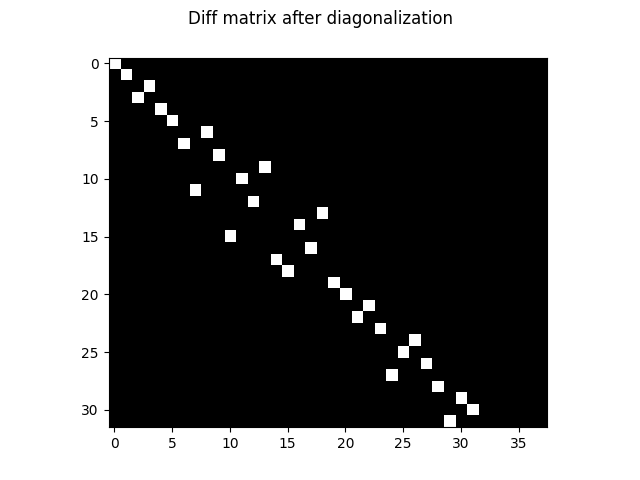
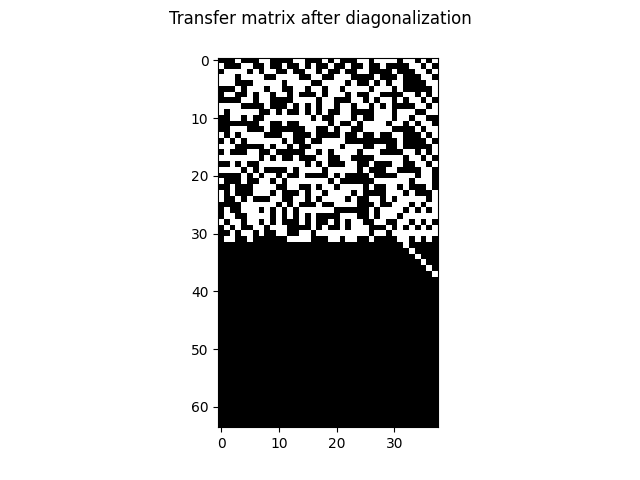
Here is how the diff and transfer matrices look like after diagonalization.

This process, it turns out, will leave us with a fully diagonal diff matrix up to columns reordering. At this point, the columns of the transfer matrix contain the coefficients of the $D_{V}^{j}$ s in the basis of the $D^{i}$ s. The next step is to reorder the columns. Because the columns are represented by unsigned integers, this can be done with a simple sort:

inline void reorder(std::vector<Column> &columns)
{
    std::sort(columns.begin(), columns.end(), [](const Column &a, const Column &b) { return a.diff < b.diff; });
}

The transfer matrix goes through the same operations as its columns are stored alongside the diff’s. After diagonalization, a few columns of the diff matrix are all-zeros, they correspond to case transformations that leave the CRC unaltered. They are hash collisions! We’re not interested in them however, as they don’t do anything, so we remove them:

inline void remove_collisions(std::vector<Column> &columns)
{
    // Remove the columns where the diff is null
    columns.erase(std::remove_if(columns.begin(), columns.end(), [](const Column &column) { return column.diff == 0; }),
                  columns.end());
}

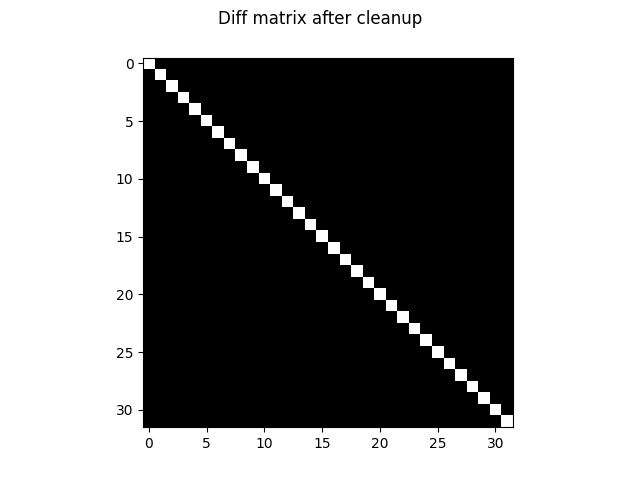
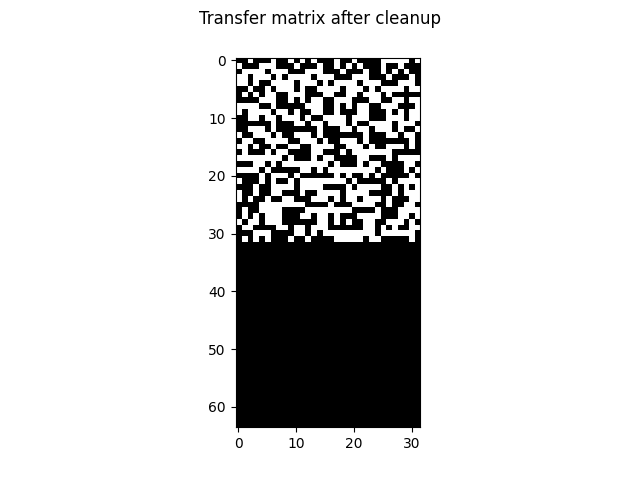
Here is how the diff and transfer matrices look like after cleanup.

Controlling the CRC

Applying a single elementary transformation

Let’s check that we can actually flip the bits one by one.

void apply_elementary_transformation(const std::string &init_str, std::vector<Column> &columns, size_t bit_index)
{
    std::string ctl_str(init_str);
    for (size_t ii = 0; ii < 32; ++ii)
        if (columns[bit_index].transfer & (1 << ii))
            ctl_str[ii] = toggle_case(ctl_str[ii]);

    uint32_t init_crc = crc32(init_str);
    uint32_t ctl_crc = crc32(ctl_str);

    std::cout << "Initial CRC: " << std::bitset<32>(init_crc) << std::endl;
    std::cout << "Final CRC:   " << std::bitset<32>(ctl_crc) << std::endl;
    std::cout << ctl_str << std::endl;
}

int main(int argc, char **argv)
{
    std::string init_str = "ThisSentenceIsLongEnoughToBeUsedAsATest";
    std::vector<Column> columns;

    compute_diffs(init_str, columns);
    diagonalize(columns);
    reorder(columns);
    remove_collisions(columns);

    apply_elementary_transformation(init_str, columns, 2);
    return 0;
}

We chose to flip the bit at position 2 (the third one from the right). So we look at the column of index 2 in the transfer matrix. This column contains the coefficients of $D_{V}^{2}$ in the basis of the $D^{i}$ s. Then if the $k$ -th bit of this column is at one, it means that we must apply the transformation $U^{k}$ to the string. We simply iterate over this column and apply the appropriate case transformations on the input string $S$ , producing the altered string $S^{'}$ . Finally, we display $C R C (S)$ , followed by $C R C (S^{'})$ , then $S^{'}$ itself. Here’s the output:

Initial CRC: 00000001010111010111101100010010
Final CRC:   00000001010111010111101100010110
THiSSeNteNCEISLOngenOughTOBeUSEdAsATest

Yep, we succeeded in flipping only the bit at position 2!

Fully controlling the CRC

Now that we can flip single bits one by one in the CRC thanks to the $D_{V}^{j}$ s, all we need to do is to compute a diff between the initial CRC and the target CRC, and for all bits that need to be flipped, apply the corresponding case transformation to our input string. These transformations can be cumulated inside a binary mask:

std::string control_crc(const std::string &init_str, const std::vector<Column> &columns, uint32_t target)
{
    uint32_t init_crc = crc32(init_str);
    uint32_t need_flip = init_crc ^ target;

    // Let's accumulate all the transformations that need to be applied in
    // a binary mask
    uint32_t mask = 0;
    for (size_t ii = 0; ii < 32; ++ii)
        if (need_flip & (1 << ii))
            mask ^= columns[ii].transfer;

    // Toggle the case at indices where the mask bits are 1
    std::string ctl_str(init_str);
    for (size_t ii = 0; ii < 32; ++ii)
        if (mask & (1 << ii))
            ctl_str[ii] = toggle_case(ctl_str[ii]);

    return ctl_str;
}

Note that we only need to touch the first 32 characters of the string. Let’s put it all together:

int main(int argc, char **argv)
{
    std::string init_str = "OhComputerTellMeWhatWeEatForDinner";
    std::vector<Column> columns;

    compute_diffs(init_str, columns);
    diagonalize(columns);
    reorder(columns);
    remove_collisions(columns);

    auto ctl_str = control_crc(init_str, columns, 0xdeadbeef);

    std::cout << "Initial string: '" << init_str << '\'' << std::endl;
    std::cout << "    -> 0x" << std::hex << crc32(init_str) << std::endl;
    std::cout << "Final string:   '" << ctl_str << '\'' << std::endl;
    std::cout << "    -> 0x" << std::hex << crc32(ctl_str) << std::endl;

    return 0;
}

Which outputs:

Initial string: 'OhComputerTellMeWhatWeEatForDinner'
    -> 0xe53388ce
Final string:   'OHcOMpuTErTELLMeWhATwEEAtFordInner'
    -> 0xdeadbeef

That’s it! We managed to find a case substitution such that the CRC evaluates to any pre-defined value. In the sample code shared on the GitHub (link below), I generate a random initial string, so you can make sure that it really works for arbitrary text.

Why should I care?

Well, say you’re (still) relying on CRC-32 as a crypto hash to authenticate files on a server. Someone who gained access to your server could potentially insert malicious bits of code in those files, and be naughty enough to alter them in such a way that the hash does not change. So you would never know by just looking at the hashes.

The affine property of the CRC was also responsible for the weak security of the WEP protocol.

For those of you who are experts in security that’s old news, I know. But I humbly hope this article contributed to give you a bit more insight into this stuff.

The full source code can be found here.

The comment section requires the Utterances cookie in order to work properly. If you want to see people's comments or post a comment yourself, please enable the Utterances cookie here.