A formula for the area enclosed by a planar Bezier curve of order n

mathematics

Wed, Dec 15, 21

Here I present a closed-form expression for the area enclosed by an arbitrary order closed Bezier curve in the plane. The formula in itself is of limited interest given that you can trivially approximate any parametrized closed curve by a polygon and compute the polygon's area instead (say with the shoelace formula), but as always in maths, the real treasure is the friends we made along the way! The proof is a bit involved, but all we need is some basic vector calculus, combinatorics and some knowledge about the Beta function.

I solved this problem in 2019 because I couldn’t find a definite answer to it after a good deal of Internet research, but surely I can’t be the first one to tackle it. I don’t quite remember why I needed this, I think I went on a side quest when designing custom variable capacitor plates or something like that, which lead nowhere. But here you go.

The problem

Say we have a closed planar Bezier curve $C$ described by $n + 1$ control points ${\vec{P}}_{i}$ with $i \in ⟦ 0, n ⟧$ . The curve being closed, we have the additional constraint that ${\vec{P}}_{0} = {\vec{P}}_{n}$ . Let $t \in [0, 1]$ be the curve parameter such that any point on the curve can be expressed as:

\begin{matrix} (1) & \vec{g} (t) = \sum_{i = 0}^{n} (\binom{n}{i}) (1 - t)^{n - i} t^{i} {\vec{P}}_{i} \end{matrix}

The curve $C = \partial Ω$ encloses a region $Ω$ of the plane. We’re looking for an expression for the area $A_{Ω}$ of this region $Ω$ .

Strategy

We’ll use a local tangent frame running along the Bezier curve together with an ad hoc vector field, to construct an integral expression of the area thanks to the divergence theorem. Then we’ll actually compute the integral to obtain a closed-form expression involving the curve’s parameters.

Maybe there’s a simpler way and I’m too braindead to notice, but that’s the path I chose.

Prerequisites

As mentioned above, we’ll need to use a fundamental result in vector calculus known as the divergence theorem. I don’t want to go into too much detail about this, you’re free to have a look at the Wikipedia article if you need a more rigorous approach, or completely skip this part if you’re already familiar with that stuff. But know that what I show here is just the tip of the iceberg!

However, do read the subsection on the Beta function, because we derive some useful equalities there.

Green’s theorem in 2D

Let $Ω$ be a region in the plane, delimited by a simple closed curve $C = \partial Ω$ that is positively oriented and piecewise smooth. Then, for any function $M$ and $N$ with continuous partial derivatives and whose domains contain $Ω$ , we have:

\begin{matrix} (2) & \oint_{\partial Ω} M d x + N d y = \iint_{Ω} (\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}) d x d y \end{matrix}

The divergence theorem in 2D

Let $d s = \sqrt{d x^{2} + d y^{2}}$ be a line element, and $\hat{n}$ the unit vector:

\begin{matrix} (3) & \hat{n} = \frac{d y {\hat{u}}_{x} - d x {\hat{u}}_{y}}{\sqrt{d x^{2} + d y^{2}}} = \frac{d y {\hat{u}}_{x} - d x {\hat{u}}_{y}}{d s} \end{matrix}

Let $\vec{F} (x, y) = P (x, y) {\hat{u}}_{x} + Q (x, y) {\hat{u}}_{y}$ be a vector field. Then:

\begin{matrix} (4) & \begin{aligned} \oint_{\partial Ω} \vec{F} \cdot \hat{n} d s & = \oint_{\partial Ω} \vec{F} \cdot (d y {\hat{u}}_{x} - d x {\hat{u}}_{y}) \\ = \oint_{\partial Ω} (P (x, y) d y - Q (x, y) d x) \end{aligned} \end{matrix}

By definition of $F$ and $\hat{n}$ . Using $2$ we get:

\begin{matrix} (5) & \begin{aligned} \oint_{\partial Ω} \vec{F} \cdot \hat{n} d s & = \iint_{Ω} (\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial x}) d x d y \\ = \iint_{Ω} \nabla \cdot \vec{F} d A \end{aligned} \end{matrix}

This last equation equates the circulation integral of a vector field around a closed curve to the flux of the divergence of the vector field through the surface enclosed by the curve. This very powerful result that is central in our proof is called the divergence theorem or Ostrogradsky’s theorem.

The Beta function

The Euler integral of the first kind (aka Beta function) is a hidden gem of mathematics, often overshadowed by its omnipresent sibling the Gamma function. It admits two complex arguments, has an integral expression, and can be expressed as a ratio of Gamma functions:

\begin{matrix} (6) & \begin{aligned} B (x, y) & ≜ \int_{0}^{1} t^{x - 1} (1 - t)^{y - 1} d t \\ = \frac{Γ (x) Γ (y)}{Γ (x + y)} & \forall x, y \in C ∣ ℜ (x) > 0, ℜ (y) > 0 \end{aligned} \end{matrix}

The Beta function has the following useful properties:

\begin{aligned} (7) & B (x + 1, y) & = B (x, y) \frac{x}{x + y} & \forall x, y \in C \\ (8) & B (x, y + 1) & = B (x, y) \frac{y}{x + y} & \forall x, y \in C \\ (9) & B (n - k + 1, k + 1) & = \frac{1}{(n + 1) (\binom{n}{k})} & \forall (n, k) \in N^{⋆} \times N \end{aligned}

We can combine these equalities to obtain two new equalities which we’ll use later on:

\begin{matrix} (10) & \begin{aligned} B (n - k + 1, k) & = B (n - k + 1, k + 1) \frac{n + 1}{k} \\ = \frac{n + 1}{k (n + 1) (\binom{n}{k})} \\ = \frac{1}{k (\binom{n}{k})} & \forall (n, k) \in N^{⋆} \times N \end{aligned} \end{matrix}

\begin{matrix} (11) & \begin{aligned} B (n - k, k + 1) & = B (n - k + 1, k + 1) \frac{n + 1}{n - k} \\ = \frac{n + 1}{(n - k) (n + 1) (\binom{n}{k})} \\ = \frac{1}{(n - k) (\binom{n}{k})} & \forall (n, k) \in N^{⋆} \times N \end{aligned} \end{matrix}

Solution

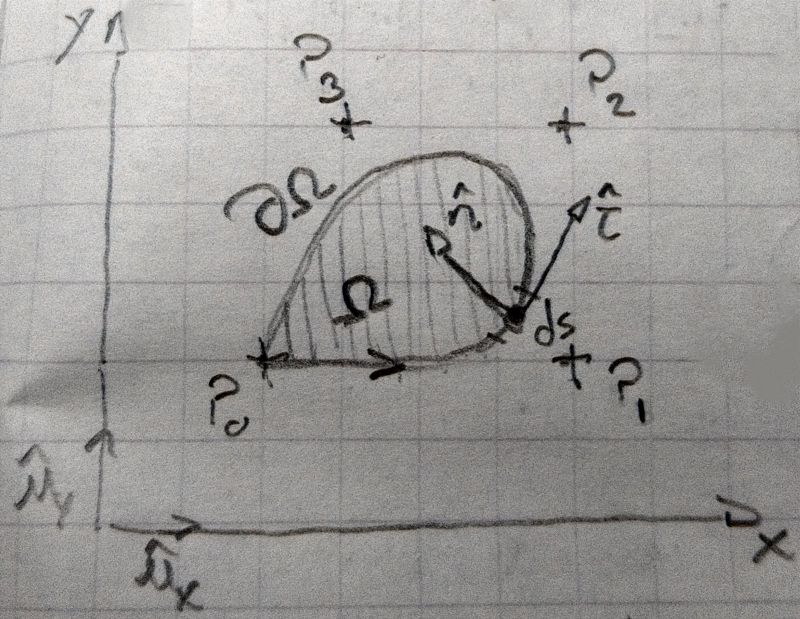
Let $(\hat{τ}, \hat{n})$ represent a local basis along the curve $C$ , $\hat{τ} (t)$ being the unit vector tangent to the curve at parameter value $t$ , and $\hat{n} (t)$ the normal unit vector.

The local basis vectors and the Bezier curve with its control points

Note that we can obtain the tangent vector easily by a $+ \frac{π}{2}$ CCW rotation. Let $R = [\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}]$ be the corresponding rotation matrix. Then we have:

\begin{matrix} (12) & \hat{τ} (t) = \frac{\partial \vec{g}}{\partial t} \end{matrix}

\begin{matrix} (13) & \hat{n} (t) = R \hat{τ} (t) = R \frac{\partial \vec{g}}{\partial t} \end{matrix}

Now, let’s consider the vector field $\vec{F} (x, y) = \frac{1}{2} [\begin{matrix} x \\ y \end{matrix}]$ . Then:

\begin{matrix} (14) & \nabla \cdot \vec{F} = 1 \end{matrix}

And the area of $Ω$ is thus:

\begin{matrix} (15) & \iint_{Ω} \nabla \cdot \vec{F} d A = \iint_{Ω} d A = A_{Ω} \end{matrix}

Let $d s$ denote the line element on the curve. Using $5$ we get:

\begin{matrix} (16) & \begin{aligned} A_{Ω} & = \oint_{\partial Ω} \vec{F} \cdot \hat{n} d s \\ = \int_{0}^{1} \vec{F} \circ \vec{g} (t) \cdot R \frac{\partial \vec{g}}{\partial t} d t \\ = \frac{1}{2} \int_{0}^{1} \vec{g} (t) \cdot \frac{\partial \vec{g}}{\partial t} d t \end{aligned} \end{matrix}

Using the definition $1$ , let’s calculate the derivative:

\begin{matrix} (17) & \begin{aligned} \frac{\partial \vec{g}}{\partial t} & = \sum_{i = 0}^{n} (\binom{n}{i}) {\vec{P}}_{i} \frac{d}{d t} ((1 - t)^{n - i} t^{i}) \\ = \sum_{i = 0}^{n} (\binom{n}{i}) (i t^{i - 1} (1 - t)^{n - i} - (n - i) t^{i} (1 - t)^{n - i - 1}) {\vec{P}}_{i} \end{aligned} \end{matrix}

Now, substituting this expression into $16$ we get:

\begin{matrix} (18) & \begin{aligned} A_{Ω} & = \frac{1}{2} \int_{0}^{1} [\sum_{i = 0}^{n} (\binom{n}{i}) (1 - t)^{n - i} t^{i} {\vec{P}}_{i}] \cdot [\sum_{j = 0}^{n} (\binom{n}{j}) (j t^{j - 1} (1 - t)^{n - j} - (n - j) t^{j} (1 - t)^{n - j - 1}) R {\vec{P}}_{j}] d t \\ = \frac{1}{2} \sum_{i = 0}^{n} \sum_{j = 0}^{n} (\binom{n}{i}) (\binom{n}{j}) \int_{0}^{1} d t [j (t^{i + j - 1} (1 - t)^{2 n - i - j}) - (n - j) (t^{i + j} (1 - t)^{2 n - i - j - 1})] {\vec{P}}_{i} \cdot R {\vec{P}}_{j} \end{aligned} \end{matrix}

The sums are finite, so they pass through the integral, no worries there. In the middle, we can split the integral into two Euler integrals of the form $6$ , allowing us to rewrite the area expression like so:

\begin{matrix} (19) & A_{Ω} = \frac{1}{2} \sum_{i = 0}^{n} \sum_{j = 0}^{n} (\binom{n}{i}) (\binom{n}{j}) [j B (2 n - i - j + 1, i + j) - (n - j) B (2 n - i - j, i + j + 1)] {\vec{P}}_{i} \cdot R {\vec{P}}_{j} \end{matrix}

Using $10$ and $11$ we can simplify things a bit:

\begin{aligned} (20) & B (2 n - i - j + 1, i + j) & = \frac{1}{(i + j) (\binom{2 n}{i + j})} \\ (21) & B (2 n - i - j, i + j + 1) & = \frac{1}{(2 n - i - j) (\binom{2 n}{i + j})} \end{aligned}

Now, substituting this into $19$ we find:

\begin{matrix} (22) & A_{Ω} = \frac{1}{2} \sum_{i, j = 0}^{n} \frac{(\binom{n}{i}) (\binom{n}{j})}{(\binom{2 n}{i + j})} [\frac{j}{i + j} - \frac{n - j}{2 n - i - j}] {\vec{P}}_{i} \cdot R {\vec{P}}_{j} \end{matrix}

Note that we have $\frac{0}{0}$ indeterminate forms for $(i = 0, j = 0)$ and $(i = n, j = n)$ , so let’s see if we can evaluate limit points for these:

\begin{matrix} (23) & \begin{aligned} lim_{j \to 0} lim_{i \to 0} [\frac{j}{i + j} - \frac{n - j}{2 n - i - j}] & = lim_{j \to 0} [1 - \frac{n - j}{2 n - j}] \\ = 1 - \frac{n}{2 n} \\ = \frac{1}{2} \end{aligned} \end{matrix}

\begin{matrix} (24) & \begin{aligned} lim_{j \to n} lim_{i \to n} [\frac{j}{i + j} - \frac{n - j}{2 n - i - j}] & = lim_{j \to n} [\frac{j}{n + j} - 1] \\ = \frac{n}{2 n} - 1 \\ = - \frac{1}{2} \end{aligned} \end{matrix}

So they exist, are of same magnitude and opposite sign. Interesting. Now, note that the binomial coefficients are equal when we set $i$ and $j$ to the two problematic configurations $(i = 0, j = 0)$ and $(i = n, j = n)$ . And also note that ${\vec{P}}_{0} \cdot R {\vec{P}}_{0} = {\vec{P}}_{n} \cdot R {\vec{P}}_{n}$ because the curve being closed we have ${\vec{P}}_{0} = {\vec{P}}_{n}$ . This means that the two end-chain contributions cancel, and we can ignore them in $22$ .

Additionally, $22$ is symmetric under swapping $i$ and $j$ : the binomial coefficients are invariant, and both the bracketted difference factor and the dot product change sign under this operation. This means we are counting contributions twice, and then divide by two, which is wasteful.

These remarks lead us to the final form:

\begin{matrix} (25) & A_{Ω} = \sum_{\begin{matrix} \binom{i = 1}{j < i} \end{matrix}}^{n} \frac{(\binom{n}{i}) (\binom{n}{j})}{(\binom{2 n}{i + j})} [\frac{j}{i + j} - \frac{n - j}{2 n - i - j}] {\vec{P}}_{i} \cdot R {\vec{P}}_{j} \end{matrix}

What a beast! Notice how $i$ starts at $1$ , $j$ at zero and stays strictly lower than $i$ . This simultaneously ensures that the end-chain contributions are not evaluated, and that we are not overcounting the contributions, allowing us to drop the $\frac{1}{2}$ factor.

Implementation

Here is a Python 3 implementation of the formula. Let’s start by importing numpy and scipy.special for the binomial coefficients:

import numpy as np
import scipy.special

Now, the function that computes $25$ . It is a straightforward nested loop with an accumulator:

def bezier_area(P):
    R = np.array([[0, 1],
                  [-1, 0]])

    N = P.shape[0]-1
    A = 0
    for ii in range(1, N+1):
        for jj in range(0, ii):
            B = scipy.special.binom(
                N, ii) * scipy.special.binom(N, jj) / scipy.special.binom(2*N, ii+jj)
            D = jj/(ii+jj) - (N-jj)/(2*N-ii-jj)
            S = np.dot(P[ii, :], np.matmul(R, P[jj, :]))
            A += B * D * S

    return A

Let’s also implement a shoelace algorithm so we can compare the two:

def approx_bezier_area(P, num_samples):
    def shoelace(x, y):
        return 0.5*np.abs(np.dot(x, np.roll(y, 1))-np.dot(y, np.roll(x, 1)))

    def bezier_interp(P, t):
        N = P.shape[0]-1
        val = np.zeros((t.shape[0], 2), dtype='float')
        for ii in range(0, N+1):
            b = scipy.special.binom(N, ii)
            c = b * np.power(t, ii) * np.power(1-t, N-ii)
            val += c[:, np.newaxis] * P[ii, :]
        return val

    N = P.shape[0]-1
    tt = np.linspace(0, 1, num_samples)
    pts = bezier_interp(P, tt)
    return shoelace(pts[:, 0], pts[:, 1])

A few things are going on. The bezier_interp() function computes the interpolated points on the curve for multiple values of the parameter t using the definition $1$ , and the shoelace algorithm was merely stolen from this Stack Overflow post. We compute num_samples values of the parameter t equally spaced between 0 and 1 with np.linspace(), and use bezier_interp() to get the interpolated points along the curve. These points form a polygon which -if the number of samples is high enough- will approximate closely the curve’s shape. Then we submit all these points to the shoelace algorithm which does its magick, and returns the polygon’s area.

Finally, we can define an arbitrary Bezier curve and run a simple test:

def main():
    P = np.array([[-0.5, -0.5], [1, -1.8], [1.5, -5],
                 [0.6, -2.3], [1, 1], [-1, 1], [-0.5, -0.5]])

    A_poly = approx_bezier_area(P, 100)
    print(f'the approximate area is {A_poly}')

    A_omega = bezier_area(P)
    print(f'the exact area is {A_omega}')


if __name__ == '__main__':
    main()

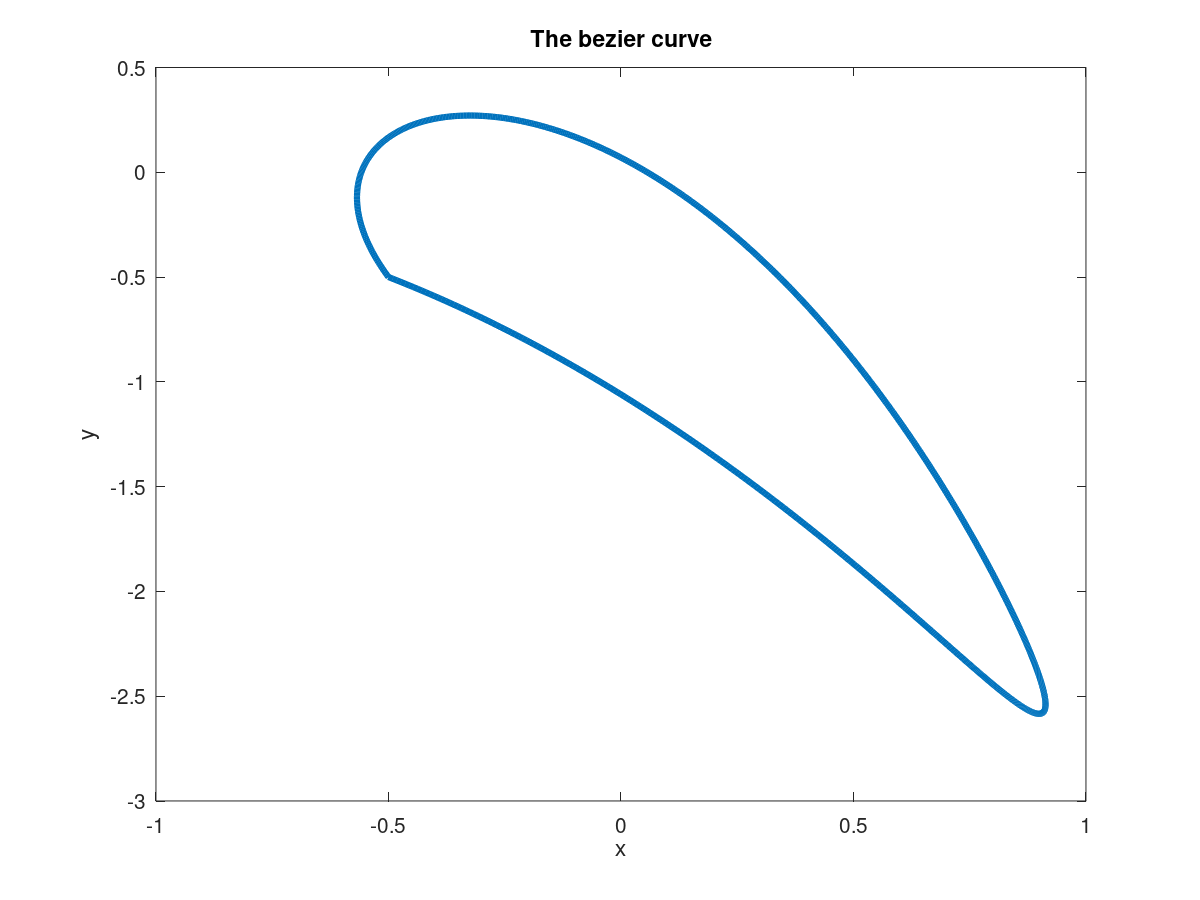
Which should output:

the approximate area is 1.3401359675890347
the exact area is 1.3405519480519479

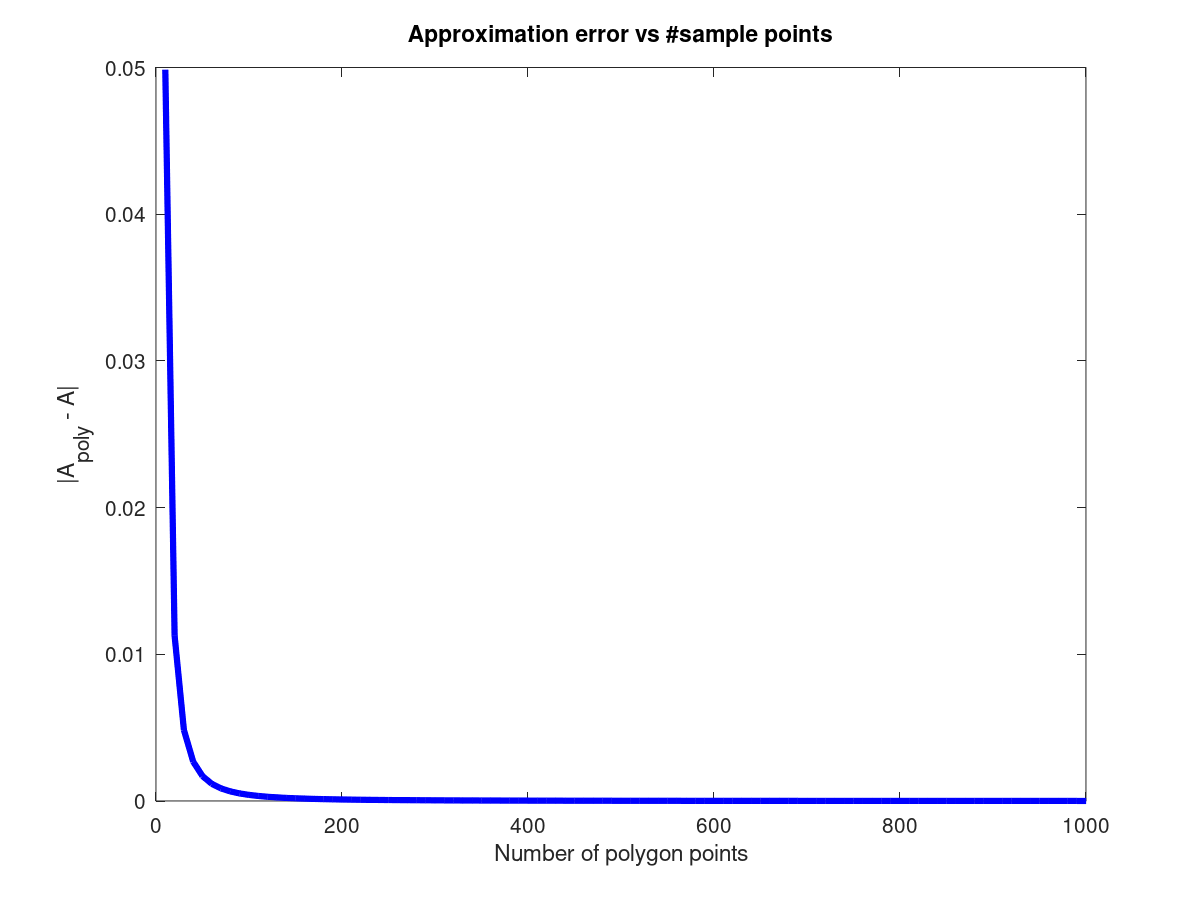
I spare you the boring details, but we can also plot the approximation error $| A_{p o l y} - A_{Ω} |$ for multiple numbers of polygon points for this specific case, and show that it vanishes exponentially as the number of points increases:

This concludes this article. One advantage of this approach -in addition to the fact that it is exact-, is that it is also faster than computing a polygon area for a few hundreds of sample points, as it only requires $\frac{n (n + 1)}{2}$ operations, with $n$ the order of the Bezier curve.

I hope you found this as interesting as I did! Maybe you came up with a simpler proof?

The full source code can be found here.

The comment section requires the Utterances cookie in order to work properly. If you want to see people's comments or post a comment yourself, please enable the Utterances cookie here.