Generalized quadratic interpolation

mathematics / engineering

Thu, Dec 23, 21

Bilinear and bicubic interpolations are the go-to methods when it comes to interpolate data on a regular grid. But experimental science being what it is, you don't always get your data nicely arranged in a rectangular 2D grid, in which case these two methods will not work. Here I present to you an extension of bilinear interpolation that works with arbitrary quadrilaterals. It is less generic than scatter interpolation, but nonetheless useful when you still have a grid, but a skewed one.

I saw this result stated in an obscure forum circa 2016 (kudos to the dude who found it), but went ahead and wrote a proof for myself. Since then I used this method a few times to interpolate data found in old chemistry books, as nearest neighbor wouldn’t cut it in terms of precision for whatever I was doing back then.

Bilinear interpolation

Interpolating a function of two variables on a regular grid can be achieved thanks to bilinear interpolation. This technique is commonly used in computer graphics to resample textures, but is often refered to as bilinear filtering in this context. We’ll succinctly explore this interpolation method without going in too much detail. The goal of this section is to highlight a few equations that we need to generalize later on.

Let $f$ be the following quadratic form:

\begin{matrix} (1) & f (x, y) = a x y + b_{x} x + b_{y} y + c, for a, b_{x}, b_{y}, c \in R \end{matrix}

Let $P_{i} = (x_{i}, y_{i})$ with $i \in ⟦ 0, 3 ⟧$ be four points in the plane, forming a rectangle. The lower left and upper right points (respectively $(x_{0}, y_{0})$ and $(x_{1}, y_{1})$ ) alone fix all the degrees of freedom of this rectangle. Then we can choose $P_{0} = (x_{0}, y_{0})$ , $P_{1} = (x_{1}, y_{0})$ , $P_{2} = (x_{1}, y_{1})$ and $P_{3} = (x_{0}, y_{1})$ . Let $z_{i}$ be a value known only at the points $P_{i}$ , that we would like to interpolate anywhere inside the rectangle. This can be done by fitting the coefficients of $1$ such that the following system of equations hold:

\begin{matrix} (2) & f (x_{i}, y_{i}) = z_{i}, \forall i \in ⟦ 0, 3 ⟧ \end{matrix}

This system can be written in matrix form:

\begin{matrix} (3) & [\begin{matrix} x_{0} y_{0} & x_{0} & y_{0} & 1 \\ x_{1} y_{0} & x_{1} & y_{0} & 1 \\ x_{1} y_{1} & x_{1} & y_{1} & 1 \\ x_{0} y_{1} & x_{0} & y_{1} & 1 \end{matrix}] [\begin{matrix} a \\ b_{x} \\ b_{y} \\ c \end{matrix}] = [\begin{matrix} z_{0} \\ z_{1} \\ z_{2} \\ z_{3} \end{matrix}] \end{matrix}

which we will denote this way:

\begin{matrix} (4) & X \vec{a} = \vec{z} \end{matrix}

and solved by matrix inversion. It can be shown that the following vector $\vec{a}$ is a solution to $4$ :

\begin{matrix} (5) & \vec{a} = [\begin{matrix} \frac{Δ f_{x y}}{δ_{x} δ_{y}} \\ \frac{Δ f_{x}}{δ_{x}} \\ \frac{Δ f_{y}}{δ_{y}} \\ z_{0} \end{matrix}] \end{matrix}

where

$δ_{x} ≜ x_{1} - x_{0}$
$δ_{y} ≜ y_{1} - y_{0}$
$Δ f_{x} ≜ z_{1} - z_{0}$
$Δ f_{y} ≜ z_{3} - z_{0}$
$Δ f_{x y} ≜ z_{0} + z_{2} - z_{1} - z_{3}$

Generalized quadratic interpolation

An optimization problem

If we don’t have a regular grid however, we can’t use bilinear interpolation anymore. Here I present a generalization of this method that works with arbitrary quadrilaterals, and admits bilinear interpolation as a special case.

Let $f$ be a generalized quadratic form:

\begin{matrix} (6) & f (x, y) = a_{x x} x^{2} + a_{x y} x y + a_{y y} y^{2} + b_{x} x + b_{y} y + c, for a_{x x}, a_{x y}, a_{y y}, b_{x}, b_{y}, c \in R \end{matrix}

Note that when $a_{x x} = 0$ and $a_{y y} = 0$ we get back the quadratic form of the bilinear interpolation $1$ . Let $P_{i} = (x_{i}, y_{i})$ with $i \in ⟦ 0, 3 ⟧$ be four points in the plane, forming an arbitrary non-degenerate quadrilateral. Let $z_{i}$ be a value known only at the points $P_{i}$ , that we would like to interpolate anywhere inside the quadrilateral. This can be done by fitting the coefficients of $6$ such that the following system of equations hold:

\begin{matrix} (7) & f (x_{i}, y_{i}) = z_{i}, \forall i \in ⟦ 0, 3 ⟧ \end{matrix}

This system can be written in matrix form:

\begin{matrix} (8) & [\begin{matrix} x_{0}^{2} & x_{0} y_{0} & y_{0}^{2} & x_{0} & y_{0} & 1 \\ x_{1}^{2} & x_{1} y_{1} & y_{1}^{2} & x_{1} & y_{1} & 1 \\ x_{2}^{2} & x_{2} y_{2} & y_{2}^{2} & x_{2} & y_{2} & 1 \\ x_{3}^{2} & x_{3} y_{3} & y_{3}^{2} & x_{3} & y_{3} & 1 \end{matrix}] [\begin{matrix} a_{x x} \\ a_{x y} \\ a_{y y} \\ b_{x} \\ b_{y} \\ c \end{matrix}] = [\begin{matrix} z_{0} \\ z_{1} \\ z_{2} \\ z_{3} \end{matrix}] \end{matrix}

which we will denote this way:

\begin{matrix} (9) & X \vec{a} = \vec{z} \end{matrix}

This linear system is underdetermined: there is an infinite number of ways to solve it. So let’s transform the problem a bit in order to find a particular solution with suitable properties. Say, for example, that we want to find the solution for which the quadratic coefficients are as small as possible. This is nice as it will ensure that $9$ will automatically degenerate to the bilinear interpolation case when the quadrilateral is a rectangle. Denote by $e = a_{x x}^{2} + a_{x y}^{2} + a_{y y}^{2}$ the energy to minimize, and by $g_{i} (x_{i}, y_{i}) = f (x_{i}, y_{i}) - z_{i}$ the constraint functions that all vanish when $9$ holds. Then our interpolation problem becomes a convex optimization problem:

\begin{matrix} (10) & minimize e = a_{x x}^{2} + a_{x y}^{2} + a_{y y}^{2} subject to g_{i} (x_{i}, y_{i}) = 0, \forall i \in ⟦ 0, 3 ⟧ \end{matrix}

Solution

Solving $10$ is done as usual via the method of Lagrange multipliers. Let $λ_{i} \in R, \forall i \in ⟦ 0, 3 ⟧$ be our four Lagrange multipliers. The Lagrangian of $10$ is simply:

\begin{matrix} (11) & L = e - \sum_{i = 0}^{3} λ_{i} g_{i} \end{matrix}

We can express this Lagrangian in terms of matrices. Let $E ≜ d i a g {1, 1, 1, 0, 0, 0}$ , then $e$ rewrites as $e = {\vec{a}}^{⊺} E \vec{a}$ . Also write $\vec{λ} = [\begin{matrix} λ_{0} \\ ⋮ \\ λ_{3} \end{matrix}]$ . Then:

\begin{matrix} (12) & L = {\vec{a}}^{⊺} E \vec{a} - {\vec{λ}}^{⊺} (X \vec{a} - \vec{z}) \end{matrix}

Then solving $10$ is equivalent to solving

\begin{matrix} (13) & \nabla L = \vec{0} \end{matrix}

with $\nabla = [\partial_{\vec{a}}, \partial_{\vec{λ}}]$ , using the short notation $\partial_{u} \equiv \frac{\partial}{\partial u}$ for the partial derivatives. Note that we differentiate with respect to vectors! This slight abuse of notation is common in theoretical physics. We could as well calculate ten partial derivatives, with respect to each component of $\vec{a}$ and $\vec{λ}$ , then group the results in vector form. But as we conveniently expressed the Lagrangian in terms of matrices and vectors, we only have these two derivatives to carry out swiftly:

$\partial_{\vec{λ}} L = - (X \vec{a} - \vec{z})$
$\partial_{\vec{a}} L = 2 E \vec{a} - X^{⊺} \vec{λ}$

Thus, $13$ rewrites as:

\begin{matrix} (14) & {\begin{cases} X \vec{a} = \vec{z} \\ 2 E \vec{a} - X^{⊺} \vec{λ} = \vec{0} \end{cases} \end{matrix}

So we recovered $9$ as our first equation, and appended a new equation to minimize $e$ . Without loss of generality, we can divide both sides of the second equation by $2$ and absorb the $- \frac{1}{2}$ factor of the second term into $\vec{λ}$ :

\begin{matrix} (15) & {\begin{cases} X \vec{a} = \vec{z} \\ E \vec{a} + X^{⊺} \vec{λ} = \vec{0} \end{cases} \end{matrix}

This gives us a nice block matrix form:

\begin{matrix} (16) & [\begin{matrix} X & 0 \\ E & X^{⊺} \end{matrix}] [\begin{matrix} \vec{a} \\ \vec{λ} \end{matrix}] = [\begin{matrix} \vec{z} \\ \vec{0} \end{matrix}] \end{matrix}

The big block matrix on the left will be called $A$ . $X$ is $4 \times 6$ , the zero block is $4 \times 4$ and $E$ is $6 \times 6$ , so $A$ is a $10 \times 10$ block lower triangular matrix with square off-diagonal partition. Because $E$ is singular and we don’t know much about $X$ , I doubt there is some nice block inversion theorem out there that allows us to calculate an exact inverse (or even a block pseudoinverse, for that matter). So the next best thing to do to solve $16$ is to compute the Moore-Penrose pseudoinverse of $A$ directly. This can be done efficiently using a singular value decomposition, but we won’t even need to touch that in our implementation thanks to numpy.linalg.

Implementation

We’ll use the method described above to interpolate colors inside an arbitrary quad:

The arbitrary quad and the colors defined only at the vertices

The implementation will be done in Python. We are going to use numpy for the linear algebra operations, matplotlib to plot things, and shapely to draw the quad.

import numpy as np
from matplotlib import pyplot as plt
from shapely.geometry import Polygon

The quadratic form $6$ will be used often. I chose to write a helper function that returns an array containing each term of the quadratic form, with all coefficients set to $1$ . To evaluate the quadratic form, a dot product of this array and a conformant array of coefficients is calculated.

def qform(xx: float, yy: float):
    return np.array([np.power(xx, 2), xx*yy, np.power(yy, 2), xx, yy, 1.0])

For better stability, the values of $x_{i}$ , $y_{i}$ and $z_{i}$ ar renormalized between $0$ and $1$ :

def normalize(X, Y, Z):
    xmin = np.min(X)
    ymin = np.min(Y)
    zmin = np.min(Z)
    Xn = X - xmin
    Yn = Y - ymin
    Zn = Z - zmin
    xmax = np.max(Xn)
    ymax = np.max(Yn)
    zmax = np.max(Zn)
    Xn /= xmax
    Yn /= ymax
    Zn /= zmax
    return (Xn, Yn, Zn, xmin, xmax, ymin, ymax, zmin, zmax)

We also define a function that takes any point and transforms it to the above normalized space:

def to_normalized_coord(X, Y, xmin, xmax, ymin, ymax):
    return ((X-xmin)/xmax, (Y-ymin)/ymax)

The extremal values of $x_{i}$ and $y_{i}$ expected as input to this function are found in the tuple returned by the normalize() function. Then we can write a function that takes the quadrilateral and the values at its vertices, and returns an interpolant:

def quad_interpolation(XX, YY, ZZ):
    # Renormalize coordinates for better stability
    Xn, Yn, Zn, xmin, xmax, ymin, ymax, zmin, zmax = normalize(XX, YY, ZZ)

    # Value vector, 4 values for the Lagrange multipliers,
    # 6 zeros for stationary points where the Lagrangian vanishes
    b = np.append(Zn, np.zeros(6))

    # We now form the matrix A of the linear system to be solved
    E = np.diag([1, 1, 1, 0, 0, 0])
    X = np.array([qform(Xn[0], Yn[0]),
                  qform(Xn[1], Yn[1]),
                  qform(Xn[2], Yn[2]),
                  qform(Xn[3], Yn[3])])
    A = np.block([
        [X, np.zeros([4, 4])],
        [E, X.T]
    ])

    # And solve the linear system for the quadratic form coefficients
    a = np.linalg.lstsq(A, b)[0]

    # Return the interpolant
    def interp(xx, yy):
        # Transform xx and yy to normalized coordinate space
        xn, yn = to_normalized_coord(xx, yy, xmin, xmax, ymin, ymax)
        # Evaluate quadratic form and transform result to original value space
        return np.dot(a[0:6], qform(xn, yn)) * zmax + zmin

    return interp

Note that using a = np.linalg.solve(A, b) instead of a call to np.linalg.lstsq() does appear to work in most cases. Now, we code the main function. We calculate an interpolant for each color channel separately, and use them to interpolate the colors inside the quadrilateral.

def main(argv):
    # These are the point coordinates for which we know a value
    X = np.array([20, 21, 29, 25], dtype='float')
    Y = np.array([1.5, 7.9, 12.154, 0.238], dtype='float')

    # These are the RGB color values for each point
    r = np.array([1.0, 1.0, 0.8, 0.8], dtype='float')
    g = np.array([0.0, 0.4, 0.0, 0.6], dtype='float')
    b = np.array([0.4, 0.0, 0.0, 0.0], dtype='float')

    # Get an interpolant for each color channel
    r_interp = quad_interpolation(X, Y, r)
    g_interp = quad_interpolation(X, Y, g)
    b_interp = quad_interpolation(X, Y, b)

    # Plot stuff
    # Construct a mesh grid
    xmin = np.min(X)
    ymin = np.min(Y)
    xmax = np.max(X)
    ymax = np.max(Y)
    xls = np.linspace(xmin, xmax, 50)
    yls = np.linspace(ymin, ymax, 50)
    xv, yv = np.meshgrid(xls, yls)

    # Interpolate colors and clamp the results between 0 and 1
    r_int = np.clip(r_interp(xv, yv), 0, 1)
    g_int = np.clip(g_interp(xv, yv), 0, 1)
    b_int = np.clip(b_interp(xv, yv), 0, 1)
    C = np.dstack((r_int, g_int, b_int))

    # Plot the quadrilateral itself
    poly = Polygon(np.dstack((X, Y))[0])
    poly_x, poly_y = poly.exterior.xy

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(poly_x, poly_y, color='black')

    # Plot each known point as a colored disk
    ax.scatter(X, Y, color=np.dstack((r, g, b))[
        0], edgecolor='black', linewidth=2, s=100)

    # Display interpolated colors as an image
    ax.imshow(C, extent=[xmin, xmax, ymin, ymax], origin='lower')
    ax.set_aspect(1.0/ax.get_data_ratio(), adjustable='box')
    plt.xlim(xmin-1, xmax+1)
    plt.ylim(ymin-1, ymax+1)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()

This should produce the following figure:

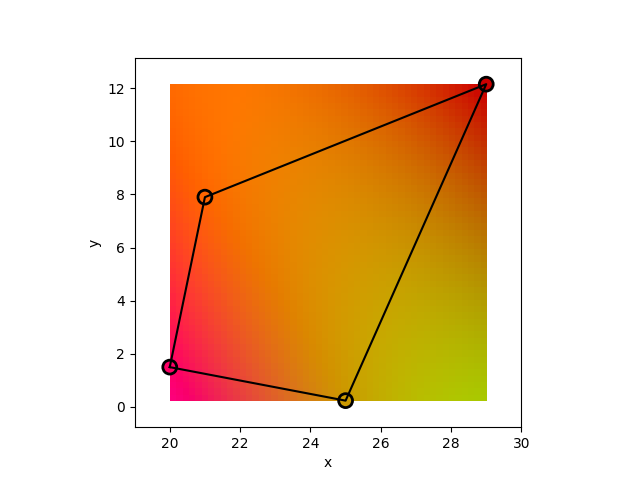
The colors are correctly interpolated inside the quadrilateral, but are also extrapolated outside!

This method works as expected, and gives a smooth result. It is of non negligible interest that, to a certain extent, it can be used to extrapolate the colors outside the quadrilateral as well. Now, to verify our previous claim that when the input quadrilateral is a rectangle, the interpolant would degenerate to the bilinear case, we simply change the values in the X and Y arrays, and repeat the experiment:

    X = np.array([20, 28, 28, 20], dtype='float')
    Y = np.array([10, 10, 15, 15], dtype='float')

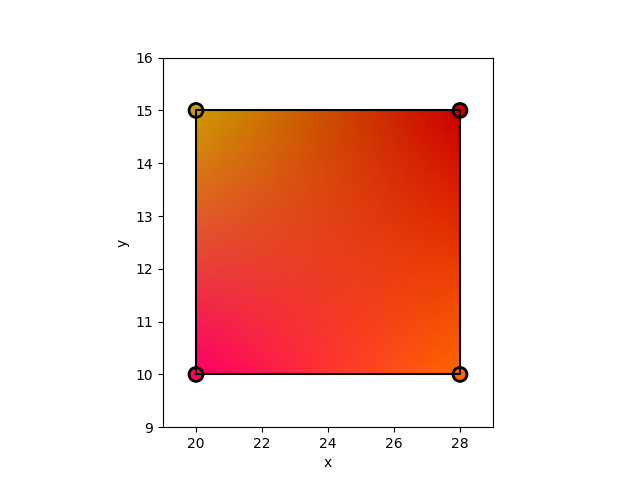
When the quadrilateral is a rectangle, we get back bilinear interpolation.

Here are the coefficient vectors $[\vec{a}, \vec{λ}]$ of the red, green and blue channels interpolants, when the quadrilateral is a rectangle. The first and third coefficients (respectively $a_{x x}$ and $a_{y y}$ ) vanish, meaning that we got back the quadratic form $1$ of the bilinear case:

[-1.052e-16  4.996e-16  2.567e-16 -9.853e-16 -1.000e+00  1.000e+00 -4.441e-16  7.910e-16 -7.216e-16  8.743e-16]
[-9.600e-16 -1.667e+00 -5.551e-17  6.667e-01  1.000e+00  7.772e-16 1.667e+00 -1.667e+00  1.667e+00 -1.667e+00]
[ 3.814e-16  1.000e+00  1.943e-16 -1.000e+00 -1.000e+00  1.000e+00 -1.000e+00  1.000e+00 -1.000e+00  1.000e+00]

I’m convinced that the same scheme can be applied to extend a bicubic interpolation too. Have you used something like that before?

The full source code can be found here.

The comment section requires the Utterances cookie in order to work properly. If you want to see people's comments or post a comment yourself, please enable the Utterances cookie here.