Arc length parametrization: Hermite spline [part 2]

mathematics / gamedev

Sun, Jan 02, 22

In a previous article we derived a few equations for the arc length parametrization of curves, and studied a specific class of curves for which a closed-form formula can be obtained. Today, we'll cover the case of Hermite splines, for which no such closed-form formula exists, and we'll see how numerical methods can be employed to solve the problem anyway. As you can guess, we'll do less maths but more code! I advise you to read at least the first section of the first part as I'm going to use it here.

Definitions

Bezier curves

I won’t give you a full overview of Bezier curves here as there is too much to talk about, read [2] for a quick jump start. But as we will use them, I should at least give some basic definitions that we can refer to.

The Bezier curves are a family of parametric curves that are wildly used in computer graphics. An order $n$ Bezier curve is specified by a set of $n + 1$ control points $\vec{P_{k}}$ , and expressed using the order $n$ Bernstein polynomials. The control points can be anything you like as long as they can be added and multiplied by a scalar, but we consider them as vectors in this article. Let $b_{k, n}$ be the Bernstein polynomials of order $n$ :

\begin{matrix} (1) & b_{k, n} (t) = (\binom{n}{k}) t^{k} {(1 - t)}^{n - k} \end{matrix}

Then an order $n$ Bezier curve of parameter $t \in [0, 1]$ is simply:

\begin{matrix} (2) & \vec{B} (t) = \sum_{k = 0}^{n} b_{k, n} (t) \vec{P_{k}} \end{matrix}

It is often desirable to work with a polynomial expansion of $2$ , which is better suited for fast interpolation on a computer:

\begin{matrix} (3) & \vec{B} (t) = \sum_{j = 0}^{n} t^{j} \vec{C_{j}} \end{matrix}

with the coefficients $\vec{C_{j}}$ given by:

\begin{matrix} (4) & \begin{aligned} \vec{C_{j}} & = \frac{n!}{(n - j)!} \sum_{i = 0}^{j} \frac{(- 1)^{i + j}}{i! (j - i)!} \vec{P_{i}} \\ = \prod_{m = 0}^{j - 1} (n - m) \sum_{i = 0}^{j} \frac{(- 1)^{i + j}}{i! (j - i)!} \vec{P_{i}} \end{aligned} \end{matrix}

This can be obtained by binomial expansion of the $(1 - t)^{n - k}$ factor in the Bernstein form. In an implementation, the $\vec{C_{j}}$ coefficients can be pre-computed once the control points are set, and the interpolations are performed using $3$ , so we just have a weighted sum of a few vectors to process.

Hermite splines

Cubic Hermite splines are used a lot as an interpolation tool, especially in game programming where they can represent agent or camera trajectories, or be used for procedural mesh generation to name a few common examples. In this context, they are often referred to as csplines. I happen to use them quite a lot to interpolate between colors too, I coded a whole daylight cycle / atmosphere system based on these a few years ago.

They are piecewise smooth curves whose sections are described by cubic polynomials. A cubic Hermite spline is fully specified by the $N + 1$ control points $\vec{P_{k}}$ it passes through, two additional free tangents at both ends, and a set of $N$ intervals $[x_{k}, x_{k + 1}]$ that serve as parameter domains on the segments. The curve obtained is smooth by construction, thanks to a constraint on tangents at the inner control points. All of the inner tangents $\vec{m_{k}}$ can indeed be computed as functions of the control points $\vec{P_{k}}$ , such that the curve and its first derivative are continuous at the control points. There is no way however to constrain the outer tangents which therefore remain free. There are many ways to compute the inner tangents, giving rise to various families of Hermite splines, but we will focus on a specific model today, called the cardinal spline.

Let $x$ denote the curve parameter. On the interval $[x_{k}, x_{k + 1}]$ , the interpolated point $\vec{P} (x)$ can be written as a polynomial function of the control points $\vec{P_{k}}$ and $\vec{P_{k + 1}}$ and the tangents $\vec{m_{k}}$ and $\vec{m_{k + 1}}$ . Let $t$ be the following affine transformation applied on $x$ :

\begin{matrix} (5) & t = \frac{x - x_{k}}{x_{k + 1} - x_{k}} \end{matrix}

This transformation maps a parameter value $x \in [x_{k}, x_{k + 1}]$ to the local parameter $t \in [0, 1]$ of the $k$ -th segment. Then we have the following definition for $\vec{P} (t)$ :

\begin{matrix} (6) & \vec{P} (t) = h_{00} (t) \vec{P_{k}} + h_{10} (t) (x_{k + 1} - x_{k}) \vec{m_{k}} + h_{01} (t) \vec{P_{k + 1}} + h_{11} (t) (x_{k + 1} - x_{k}) \vec{m_{k + 1}} \end{matrix}

where the $h_{\cdot \cdot}$ functions are the following basis polynomials:

\begin{matrix} (7) & \begin{aligned} h_{00} (t) & = 2 t^{3} - 3 t^{2} + 1 \\ h_{10} (t) & = t^{3} - 2 t^{2} + t \\ h_{01} (t) & = - 2 t^{3} + 3 t^{2} \\ h_{11} (t) & = t^{3} - t^{2} \end{aligned} \end{matrix}

As stated previously, we will restrict ourselves to the family of cardinal splines, whose inner tangents $\vec{m_{k}}$ are modelled this way:

\begin{matrix} (8) & \vec{m_{k}} = (1 - c) \frac{\vec{P_{k + 1}} - \vec{P_{k - 1}}}{x_{k + 1} - x_{k - 1}}, for c \in [0, 1] \end{matrix}

The parameter $c$ called the tension controls the lengths of the tangents. The higher $c$ is, the tighter the bends, and when $c = 1$ the spline degenerates to a broken line.

By expansion of $1$ we can show that our basis functions $h_{\cdot \cdot}$ can be expressed in terms of the order $3$ Bernstein polynomials:

\begin{matrix} (9) & \begin{aligned} h_{00} (t) & = b_{0, 3} (t) + b_{1, 3} (t) \\ h_{10} (t) & = \frac{1}{3} b_{1, 3} (t) \\ h_{01} (t) & = b_{3, 3} (t) + b_{2, 3} (t) \\ h_{11} (t) & = - \frac{1}{3} b_{2, 3} (t) \end{aligned} \end{matrix}

This means that our segments can in fact be expressed as Bezier curves! Indeed, the following set of Bezier control points:

\begin{matrix} (10) & {\vec{P_{k}}, \vec{P_{k}} + \frac{1}{3} (x_{k + 1} - x_{k}) \vec{m_{k}}, \vec{P_{k + 1}} - \frac{1}{3} (x_{k + 1} - x_{k}) \vec{m_{k + 1}}, \vec{P_{k + 1}}} \end{matrix}

when substituted into $2$ and using $9$ , define a cubic patch of the form $6$ between the Hermite control points $\vec{P_{k}}$ and $\vec{P_{k + 1}}$ . The two inner Bezier control points of $10$ determine the tangents at the segment’s ends.

I find it more useful to define Hermite splines in terms of Bezier patches as it opens the way to useful algorithms such as De Casteljau splitting, and allows to reuse an existing Bezier spline implementation (if you happen to have one in your codebase, which most of the game devs do). So that’s a design choice I’m going to make in the following implementation.

Arc length parametrization?

Let’s see if we can find a closed-form formula for the arc length of an order $3$ Bezier curve $\vec{B} (t)$ . Going through the maths developped in part 1 and using $3$ , the arc length function is written as:

\begin{matrix} (11) & s (t) = \int_{0}^{t} ‖ \frac{d \vec{B} (u)}{d u} ‖ d u = \int_{0}^{t} ‖ \vec{C_{1}} + 2 u \vec{C_{2}} + 3 u^{2} \vec{C_{3}} ‖ d u \end{matrix}

We can already stop right there, because for arbitrary control points, the norm in the integrand will evaluate to the square root of a degree $4$ polynomial. This is what is called an elliptic integral, and there’s nothing we can do to express it using elementary functions. Of course, this implies that there is no closed-form formula for the inverse $t (s)$ either. Then if we can’t do it for the spline segments, we surely can’t do it for the whole spline: we’re toast. And this situation is far from uncommon it turns out: even a simple ellipse -that is not also a circle- does not admit a closed-form formula for its length, precisely because the arc length integral is of this form (that’s why it is called an elliptic integral, by the way).

This doesn’t mean however, that we can’t evaluate or approximate this beast numerically. The spline does have a length of course, it’s just not expressible in terms of elementary functions. If we can compute a series of values $s_{i}$ that approximate $s (x)$ close enough in $[0, 1]$ , a numerical method can be used to compute a series of values $x_{i}$ that approximate $x (s)$ , and we’re going to do exactly this!

Implementation

You can find my original C++ implementation in my personal GitHub here, and an example on how to use it here. This is part of a library project called Kibble that I use mainly for game development. This implementation has much more features than what I’ll cover in this article, for example, it handles the computation of first and second derivatives along the spline, De Casteljau splits and can perform accurate length estimations. So it’s a beast, but a well documented one.

The demo I’m showcasing today will be done in Python with numpy. numpy shares a lot of spirit with Matlab, and its constructs tend to hide some loops as we address vectors and matrices as a whole. So be aware of this conceptual leap if you’re coming from the lands of C / C++ / Rust / Java.

We will start by coding Bezier splines that we’ll then use as segments in a Hermite spline implementation. The arc length parametrization will be handled by a wrapper around a Hermite spline.

Choices

We will consider Hermite splines defined using $N + 1$ control points, which means there are $N$ segments. Without loss of generality, we will assume that $x \in [0, 1]$ for our curve parameter $x$ . We will also impose that all the intervals $I_{k} = [x_{k}, x_{k + 1}]$ are of same length, and as such, $Δ x = x_{k + 1} - x_{k} = \frac{1}{N}$ is constant for all $k$ . Then all the intervals $I_{k}$ partition the unit interval uniformly. This simplifies a lot of things in the equations above and therefore in the implementation itself. But what works for me may not work for you, just go back to the general definitions if you want to do something fancier.

As the tangents $\vec{m_{k}}$ always appear multiplied by a factor $Δ x$ in $6$ and $10$ , I chose to pre-multiply them by $Δ x$ during their calculation, which simplifies their expressions even more. You’ll see a note explaining the details in the relevant section down below.

Cubic Bezier spline

First, we should write code for our Hermite spline segments. Each segment of a Hermite spline can be defined as a cubic Bezier spline as we saw previously. We are going to define a generic Bezier spline in this section, and when the time comes to use it, we are going to feed it four control points so it’s always cubic (remember that the order of a Bezier spline is the number of control points minus one). Thanks to $4$ we can compute the coefficients $\vec{C_{j}}$ in advance, so when we sample the Bezier spline, we only need to calculate the weighted sum of four precomputed vectors:

class BezierSpline:
    def __init__(self, control_points):
        self.control_points = control_points
        self.calculate_coefficients()

The calculate_coefficients() function will take care of computing the $\vec{C_{j}}$ coefficients:

    def calculate_coefficients(self):
        self.coefficients = np.zeros(self.control_points.shape)
        N = self.control_points.shape[0]
        prod = 1
        for jj in range(N):
            # Product from m=0 to j-1 of (n-m)
            prod *= N - jj if jj > 0 else 1
            # Weighted sum from i=0 to j of the control points
            ii = np.array(range(jj+1))
            factor = np.power(-1, ii+jj) * prod / (scipy.special.factorial(ii)
                                                   * scipy.special.factorial(jj - ii))
            self.coefficients[jj, :] = np.dot(
                factor, self.control_points[0:jj+1])

It looks heavy, but it is a direct implementation of $4$ . Of course, if you’re going to change the control points dynamically, you must recalculate the coefficients. Now, to interpolate along the Bezier spline, we define this function using $3$ :

    def sample(self, tt):
        N = self.control_points.shape[0]
        tpow = np.power(tt[:, np.newaxis], np.array(range(N)))
        return np.matmul(tpow, self.coefficients)

The np.newaxis and np.matmul shenanigans allow us to feed an array of parameter values as tt, so we only need to call this function once. But under the hood it will evaluate the power series $3$ for each value of tt, that’s all. You will need to modify the code a little bit if you want it to work with scalars as control points. And we’re done for this part! Let’s build and sample a cubic Bezier spline to test this:

def main(argv):
    control_points = np.array([
        [0, 0], [0.5, 5], [5.2, 5.5], [3, 2.2]
    ])
    B = BezierSpline(control_points)

    tp = np.linspace(0, 1, 50)
    rp = B.sample(tp)

    # [Plot stuff]

The plotting code was omitted, but you can find it in the full source code (link below). This is what we get:

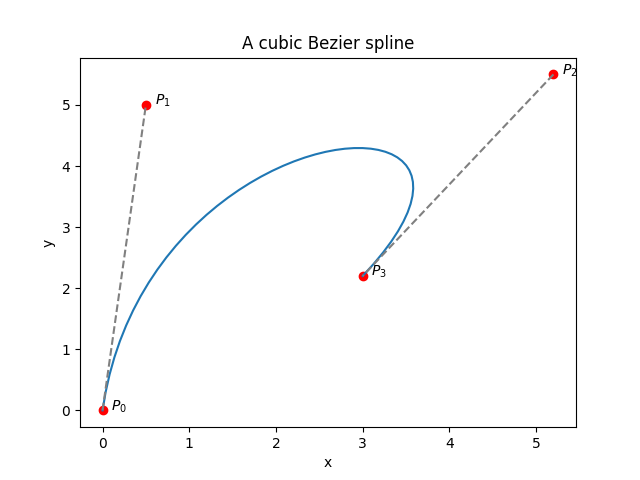
In blue: the cubic Bezier spline. The red dots are the control points. The dashed gray lines connect the inner control points $P_{1}$ and $P_{2}$ to the outer control points $P_{0}$ and $P_{3}$ respectively.

which is exactly what we expect. The curve passes through the first and last control points, and is “attracted” to the control points in the middle. More precisely, if you draw a line between the control points $P_{1}$ and $P_{0}$ , you observe that this line is tangent to the curve at $P_{0}$ . So $P_{1}$ imposes a tangent at $P_{0}$ . Same spiel for $P_{2}$ and $P_{3}$ respectively. In fact, specifying the inner control points in a cubic Bezier spline is equivalent to specifying the tangents at both ends. The size of the tangents matter too: the lengthier the tangent, the more the curve will stick to it. This is important to understand, as these tangents will play a crucial role in the next part.

Because of the way we defined the Bezier spline, you could feed it control points in 3D space (or even 5D if you ascended to a higher plane of existence) and it would work the same. Neat. But in practice, you will need to interpolate other things than just vectors, quaternions come to mind. In this case, you will have to adapt your code to perform a Slerp for example, read [1] for a detailed explanation on how to construct a so-called quaternion curve.

Cubic Hermite spline

Now, we can use our BezierSpline class as a building block for Hermite splines. We will restrict ourselves to the cardinal splines family that we discussed in the first section, which means that we use $8$ as a model to choose the tangents at each inner control point. However, the tangents at both ends of the Hermite spline remain free, and we must specify them during construction. The construction of a generic Hermite spline will then require three pieces of data:

The control points which the spline must pass through
The unconstrained tangents at both ends
The tension parameter $c$

Our __init__() method should calculate the tangents at each control point (except at the beginning and end of the curve, where they are manually specified), and also initialize a BezierSpline object for each segment:

class HermiteSpline:
    def __init__(self, control_points, tension, free_tangents):
        self.control_points = control_points
        self.calculate_tangents(tension, free_tangents)
        self.calculate_segments()

    def size(self):
        return self.control_points.shape[0]

The tangents are stored in a numpy array as usual. To calculate the (inner) tangents, we just use the formula $8$ for generic cardinal splines:

    def calculate_tangents(self, tension, free_tangents):
        # Initialize start and end tangents
        self.tangents = np.zeros(self.control_points.shape)
        self.tangents[0] = (1 - tension) * free_tangents[0]
        self.tangents[-1] = (1 - tension) * free_tangents[1]

        # Formula for a generic cardinal spline
        for ii in range(1, self.size() - 1):
            self.tangents[ii] = (1 - tension) \
                * (self.control_points[ii+1] - self.control_points[ii-1])

Detail [click to expand]

Because we are using segment intervals of constant size, we have that $Δ x = x_{k + 1} - x_{k} = \frac{1}{N} \forall k$ , with $N + 1$ the number of control points. Then, according to $8$ , the tangents show a $2 Δ x$ in the denominator. As we chose to pre-multiply the tangents by $Δ x$ during their calculation, a $2$ should remain in the denominator. But I found that it only limits the action of the tension parameter, so I simply got rid of it. Sue me!

Also note that the free tangents get multiplied by $1 - c$ like the rest. I found that the different curves obtained by varying $c$ stay more coherent this way.

And each segment is calculated according to $10$ :

    def calculate_segments(self):
        self.segments = []
        for ii in range(self.size()-1):
            bezier_control_points = np.array([
                self.control_points[ii],
                self.control_points[ii] + self.tangents[ii] / 3,
                self.control_points[ii+1] - self.tangents[ii+1] / 3,
                self.control_points[ii+1]
            ])
            self.segments.append(BezierSpline(bezier_control_points))

Technically, for each segment, we are defining four control points for the underlying Bezier spline, two of which are successive control points of the Hermite spline, and the other two in the middle are constrained by the tangents. Don’t get mixed up between “Hermite control points” on the one hand, and “Bezier control points” on the other.

Now, this is where things get wild, and I apologize for that in advance. Our Hermite spline admits a parameter $x$ between $0$ and $1$ . Each segment of the Hermite spline also admits a parameter $t$ in the same range, and we will refer to it as the local space parameter. If we want to sample the Hermite spline at a given parameter value, we need in fact to sample the appropriate Bezier spline segment at the appropriate local space parameter value. So we must:

Find the segment index $k$ corresponding to the value of $x$
Calculate the local space parameter $t$ as a function of $k$ and $x$

Given that there are $N$ segments, the index $k$ can be calculated like so:

\begin{matrix} (12) & k = min (⌊ N x ⌋, N - 1) \end{matrix}

with $⌊ \cdot ⌋$ the floor function. At $x = 1$ only, the value output by the floor function will be $N$ which is out of bounds in our array of segments. So we need to make sure that the value of $k$ stays within bounds, hence the $min$ .

To calculate $t$ , we just need to extract the fractional part of $N x$ :

\begin{matrix} (13) & t = N x - k \end{matrix}

Proof [click to expand]

Because we are using segment intervals of constant size, we have that

Δ x = x_{k + 1} - x_{k} = \frac{1}{N} \forall k

. Given the index

k

of the segment, we have that

x_{k} = \frac{k}{N}

. Substituting into

5

gives:

\begin{matrix} (14) & t = \frac{x - x_{k}}{x_{k + 1} - x_{k}} = N (x - \frac{k}{N}) = N x - k \end{matrix}

Now, because we are using numpy for this demo, we must make this work for arbitrary arrays of parameter values xx. So we write a helper function that takes in xx as an input, and spits out one pair $(k, t (k, x))$ for each value $x$ of xx:

    def to_local_space(self, xx):
        # Find segment index corresponding to each value of xx
        tclip = np.clip(xx, 0, 1)
        idxs = np.clip(np.floor((self.size()-1) * tclip), 0, self.size() - 2)
        # Convert xx to local parameter value
        tt = xx * (self.size()-1) - idxs

        # Return an array that aggregates segment indices and local parameter value
        return np.dstack((idxs, tt))[0]

The sample() function of the BezierSpline expects an array of $t$ as input, so we must group the local space parameter values by index, and submit each group to the appropriate segment:

    def sample(self, xx):
        # Group local segment parameter values by index
        loc = self.to_local_space(xx)
        unique = np.unique(loc[:, 0], return_index=True)
        seg_tt = np.split(loc[:, 1], unique[1][1:])

        # Sample each segment
        return np.concatenate([
            self.segments[int(idx)].sample(tloc)
            for idx, tloc in zip(unique[0], seg_tt)
        ])

Finally, we concatenate all the sample values returned by each segment. I know it’s a tough one to digest (writing it was no less of an arduous task), but take your time, add a few print statements here and there, and you’ll see that it makes sense. The C++ implementation I mentioned at the beginning of the section is much more straightforward in that regard (albeit way lengthier in general), so maybe take a look at it.

Still with me? Let’s display a Hermite spline:

    control_points = np.array([
        [0, 0], [0.5, 5], [5.2, 5.5], [3, 2.2]
    ])
    free_tangents = np.array([
        [0,3], [-4,0]
    ])
    H = HermiteSpline(control_points, 0, free_tangents)

    tp = np.linspace(0, 1, 50)
    rp = H.sample(tp)

    # [Plot stuff]

which should output:

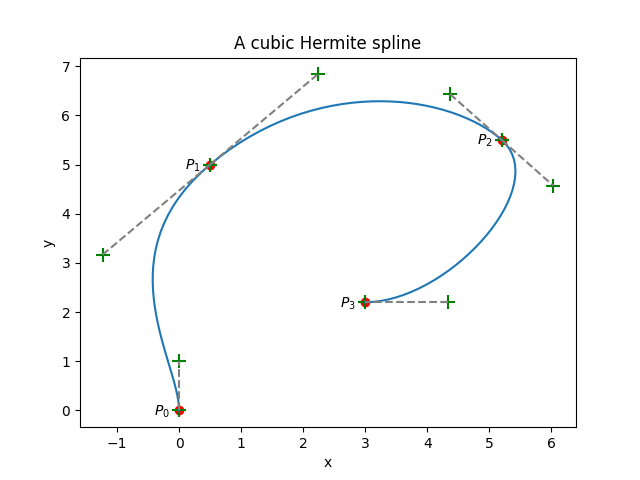
In blue: the cubic Hermite spline. The red dots are the control points. The green crosses are the segments’ (Bezier) control points, and the dashed gray lines show the tangents. The value of $0$ was chosen for the tension parameter $c$

I chose the same values for the control points as before, not in an attempt to confuse you even more, but to make more obvious the difference with a Bezier spline: the Hermite spline passes through all of its control points. This one has three segments, all of which begin and end at a Hermite spline control point. As you can see, the inner control points of each segment (shown in green) prescribe a tangent at each segment end. Let’s plot Hermite splines using the same set of control points and free tangents for multiple values of $c$ to observe the effect it has:

The hotter the color, the higher the tension

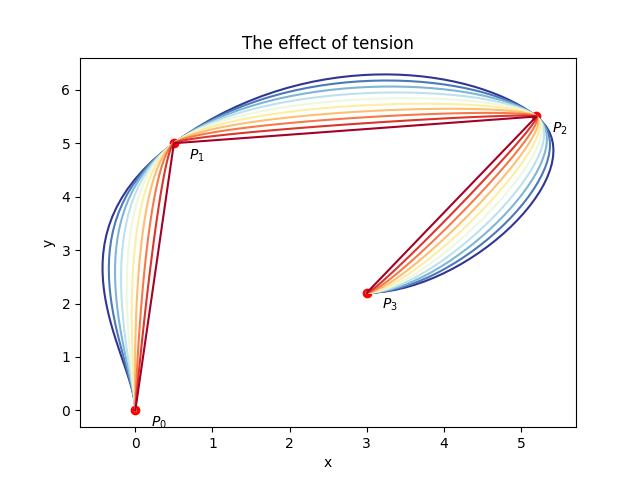
It’s as if the curve had some elastic quality to it, and we were pulling it from one end, the other being attached, hence the name “tension” for $c$ . When the tension is equal to $1$ , by $8$ all the tangents vanish, and the spline looks like a broken line.

Arc length parametrization

As stated earlier, there is no closed-form expression for the arc length function of a Hermite spline, so the next best thing to do is to sample the spline at multiple locations and approximate the arc length numerically at these locations. Then, we can use a binary search algorithm to invert the arc length table numerically, giving us an inverse arc length table that we will use as a lookup table (LUT) for uniform sampling.

First, let’s define another class that will wrap a HermiteSpline and allow uniform sampling:

class ArclenHermiteSpline:
    def __init__(self, spline, samples):
        self.spline = spline
        self.calculate_lengths_iterative(samples)
        self.invert_arc_length(samples)

The samples constructor argument specifies the number of sample points along the spline used for the calculation of the arc length table.

Getting an arc length table

There are multiple ways to approximate the arc length along the spline. The easiest is to sample the spline densely enough, and compute pairwise Euclidean distances between consecutive points. Then, a prefix sum of these distances is performed, and we obtain the cumulative distance at each sample point. This can be done succinctly in Python using array slices and numpy.cumsum():

    def calculate_lengths_iterative(self, samples):
        # Sample the Hermite spline
        tp = np.linspace(0, 1, samples)
        rp = self.spline.sample(tp)
        # Calculate Euclidean distances between consecutive pairs of points
        distances = np.zeros(tp.shape)
        distances[1:] = np.linalg.norm(rp[1:, :] - rp[:-1, :], axis=1)
        # The arc length table is the prefix sum of these distances
        self.arc_length = np.cumsum(distances)

If the sample points are densely packed along the curve, the lengths will be approximated correctly. If you need more precision, consider using a De Casteljau split algorithm on the spline segments. This is possible because we defined segments as Bezier splines! Maybe I’ll write about this in a future article.

Inverting the arc length table

So we have a table self.arc_length containing the arc lengths $s$ of the spline for multiple sample points. This table approximates the arc length function $s (x)$ , so in essence, the indices of this table should correspond to the parameter $x$ . Let’s call $s_{i}$ the value in this table corresponding to the index $i$ .

If we want to invert $s (x)$ numerically, that is, to find an approximation for $x (s)$ , then for multiple values $s$ of the arc length we must find the index $i$ such that $s_{i}$ is the largest value that verifies $s_{i} \leq s$ . To rephrase this, we are looking for the largest $s_{i}$ that is smaller than $s$ . This is a job for a binary search algorithm:

    def binary_search(self, target, last_idx):
        lb = last_idx
        ub = self.arc_length.shape[0]
        idx = lb

        while lb < ub:
            idx = lb + (ub - lb) // 2
            if self.arc_length[idx] < target:
                lb = idx + 1
            else:
                ub = idx

        return idx - 1 if self.arc_length[idx] > target else idx

Basically, we initialize a lower bound lb and an upper bound ub to cover the whole search interval, the index we’re looking for being somewhere inbetween. Then we iteratively narrow down this interval until lb and ub converge to the same integer. At this point, we know that this integer is either the index we’re looking for, or the integer just above that, and we decide based on an ultimate comparison test.

This algorithm will be called iteratively for monotonically increasing values of $s$ . Because the values $s_{i}$ are also monotonically increasing, we know that at a given iteration, we won’t find our target value $s$ before the index returned by the previous iteration, so we can cut down costs by initializing the lower bound to this last index instead of $0$ as we would normally do.

Let’s now write a function that takes in a normalized arc length parameter $\overset{―}{s} \in [0, 1]$ and returns an approximation for the curve parameter $x$ :

    def arclen_remap(self, s_bar, last_idx):
        # Arc length from normalized arc length
        ss = np.clip(s_bar, 0, 1) * self.arc_length[-1]
        # Get the index of the largest arc length value that is
        # smaller than our target value ss
        idx = self.binary_search(ss, last_idx)
        max_idx = self.arc_length.shape[0]-1

        if idx == max_idx:
            return 1, idx

        # The distance covered in the LUT by the binary search
        # algorithm is a measure of the inverse of the arc length
        len_before = self.arc_length[idx]
        len_after = self.arc_length[idx+1]
        len_segment = len_after - len_before
        frac = (ss - len_before) / len_segment
        xx = (idx + frac) / max_idx
        return xx, idx

First we compute $s$ by multiplying $\overset{―}{s}$ by the total length $L$ of the spline ( $L$ is the last element of the arc lengths array self.arc_length). Then we find the index idx in the arc lengths table thanks to our binary_search() function. We could return idx / max_idx which corresponds to the fraction of the table size covered by idx, but this is too crude of an approximation, and we can do better that that.

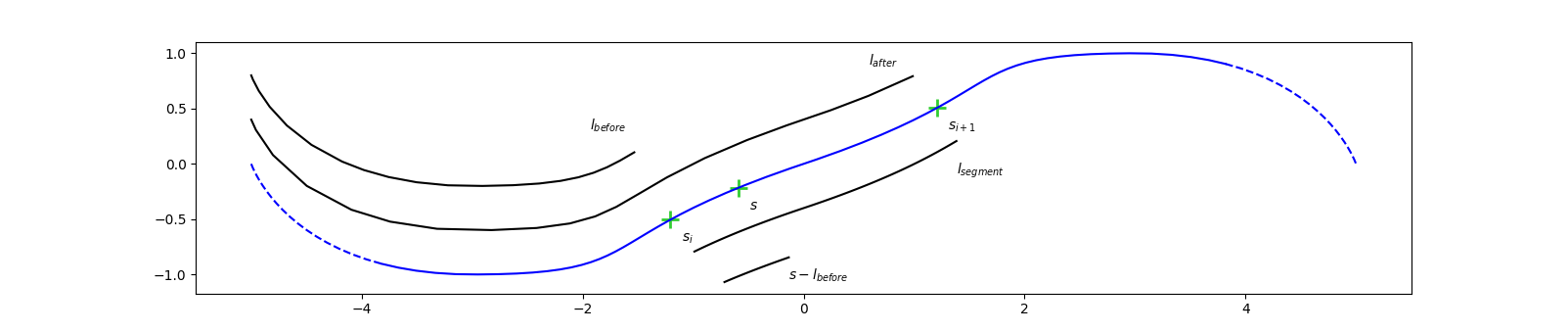
We know that our target length $s$ will be located between $s_{i}$ (self.arc_length[idx]) and $s_{i + 1}$ (self.arc_length[idx+1]) by construction. We can then compute a fractional part frac between $0$ and $1$ that tells us exactly where $s$ is located within this interval. Then we return (idx + frac) / max_idx as our approximation for $x$ .

We also take care of returning idx for the next binary search iteration to use.

Finally, we can write the invert_arc_length() used by the constructor, to build the arc length lookup table:

    def invert_arc_length(self, samples):
        last_idx = 0
        self.lut = np.zeros(samples)

        # Build the lookup table iteratively
        for ii in range(samples):
            s_bar = ii / (samples - 1)
            self.lut[ii], last_idx = self.arclen_remap(s_bar, last_idx)

        # Repeat the last value in order to avoid an out of bounds
        # error during sampling
        self.lut = np.append(self.lut, self.lut[-1])

That’s pretty straightforward: for multiple values of $\overset{―}{s}$ homogeneously distributed in $[0, 1]$ we use the arclen_remap() function to compute the corresponding values of the curve parameter $x$ . The last line of code seems out of place, but we’ll discuss its raison d’être soon enough.

All that is left to do is write a sample() function that will remap an array of $\overset{―}{s}$ to their corresponding values of $x$ and sample the Hermite spline with it:

    def sample(self, s_bar):
        # Get the values xx of the curve parameter corresponding
        # to the normalized arc lengths s_bar
        sclip = np.clip(s_bar, 0, 1)
        max_idx = self.lut.shape[0] - 2
        idxs = np.floor(sclip * max_idx).astype(int)
        alpha = max_idx * sclip - idxs
        xx = (1-alpha) * self.lut[idxs] + alpha * self.lut[idxs + 1]

        # Sample the spline
        return self.spline.sample(xx)

For all values of $\overset{―}{s}$ we compute an index $i$ in the lookup table:

\begin{matrix} (15) & i = ⌊ i_{m a x} \overset{―}{s} ⌋ \end{matrix}

Then, the corresponding $x$ must be between $x_{i}$ (self.lut[i]) and $x_{i + 1}$ (self.lut[i + 1]), and we use a simple lerp to obtain a better approximation:

\begin{matrix} (16) & α = i_{m a x} \overset{―}{s} - i \end{matrix}

\begin{matrix} (17) & x \approx (1 - α) x_{i} + α x_{i + 1} \end{matrix}

Because we are querying self.lut[i + 1] in this function, care must be taken so as to avoid an out of bounds error. As a simple fix, we repeated the last value $x_{m a x}$ of the lookup table in the invert_arc_length() function, so $17$ returns exactly $x_{m a x}$ when $\overset{―}{s} = 1$ .

Let’s see how it looks:

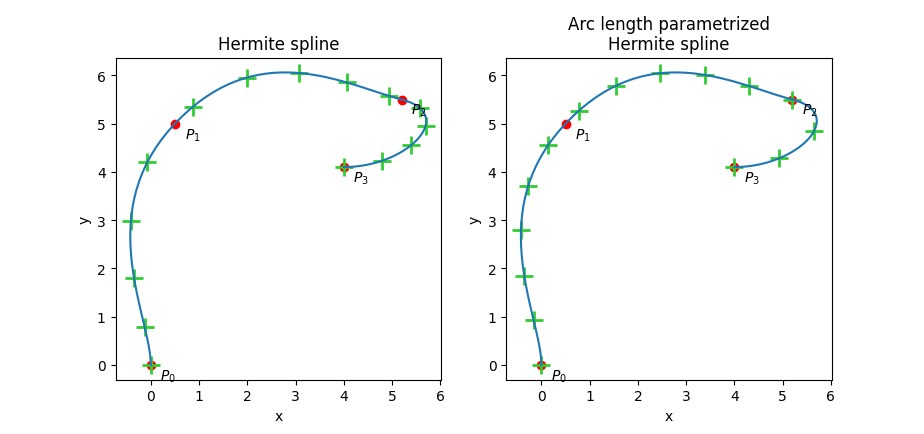
On the left: a Hermite spline in blue, with 15 sample points (shown in green) using the default parametrization. The input parameter values are homogeneously chosen in $[0, 1]$ . On the right: the same spline, but using the arc length parametrization. The control points are displayed as red dots.

I modified the control points a bit as compared to the previous figure, so the last segment is shorter and the last bend tighter. This makes more obvious the uniformity defect of the default parametrization. You can see on the other hand that sampling the curve with an arc length parametrization gives equally spaced sample points.

This concludes this article. If you made it here, congratulations! I know it’s a tough subject to wrap one’s head around.

Sources

[1] Myoung-Jun Kim, Myung-Soo Kim, and Sung Yong Shin (1995). “A General Construction Scheme for Unit Quaternion Curves with Simple High Order Derivatives”
[2] Bezier Curves from the Ground Up - Jamie Wong’s article on Bezier curves, with awesome animations.

The full source code can be found here.

The comment section requires the Utterances cookie in order to work properly. If you want to see people's comments or post a comment yourself, please enable the Utterances cookie here.